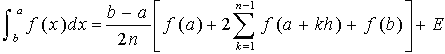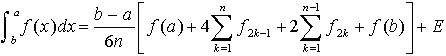|
Dedicatoria
Hay dos cosas inmutables: Las cadenas de texto en .NET y el empeño de “el Guille” en servir al mundo de la programación. Por está fecha celebramos el décimo aniversario de “el Guille” y es un honor para a mi contribuir a su portentoso sitio Web con un articulo. Mis más cordiales felicitaciones Guille.
Introducción
Los delgados es una característica de los lenguajes de programación ciertamente avanzada que usan los programadores que solucionan problemas de propósito general. Los programadores de producción tienen una visión mas bien lejana del poder de los delegados ya que por lo general se ocupan de problemas específicos. Los programadores de C++ conocen bien la técnica, la han usado desde hace años. Por ejemplo el sistema operativo Windows basa fuertemente su código en punteros a funciones, es decir en delegados. Los lenguajes actuales de .NET disponen esta característica de manera avanzada y segura. Así pues, los delegados se pueden usar en problemas de aplicaciones específicas.
Definición de Delegados
En lenguajes .NET un delegado es un tipo que hace referencia a un método. Se define y trata como un tipo de variables especial. En .NET los delegados poseen seguridad de tipos. Esto es particularmente elegante porque pone a alto nivel su uso. Con los delegados de pueden definir métodos de devolución de llamada. Por ejemplo Ajax .NET o ‘Atlas’ basan virtuosamente su código en delegados. En fin, en la MSDN puede encontrar la guía pertinente para usar delegados, use esta dirección: http://msdn2.microsoft.com/es-es/library/ms173171.aspx
Un ejemplo Concreto
Las aplicaciones que solucionan problemas de matemática aplicada son intemporales. He retomado un articulo que escribir a principios de mil novecientos algo, acerca de la solución de integración numérica, escrito para VB6, lo reescribí en .NET, y lo enfoque a usar delegados. Se percibe su robusta transformación. Una de mis ideas finales debe ser poder una función integrador con menos líneas de código y general. El corolario sería así::
“Déme la integral de ésta función entre éste intervalo, con frecuencia tal, usando el método deseado…”
Quizás el código final luzca así::
Lo cual en palabras “explicitas” podría decir:
Déme la integral de la función ‘Reciproco’, entre 1.0 y 2.0, con una frecuencia de 10 intervalos, usando la Regla de los Trapecios.
Aquí Integrator es una función capaz de resolver una integración numérica de una función con nombre, en este caso Reciprocal (reciproco es la función matemática que evalúa 1 / x), pasada como parámetro, a través de un método con nombre, TrapeziumsRule (la regla de los trapecios es una técnica numérica para solucionar integrales), también pasado como parámetro. Esta línea de código, que se lee con intuición, tiene un código ciertamente avanzado, que se va a explicar en este articulo.
De la misma forma, se podría aplicar el modelo del ejemplo a muchos casos de problemas de matemática aplicada de manera más general.
Existe una característica aun más avanzada con .NET y son los Métodos Anónimos. Lo cual también voy a explicar con ejemplo al final de este articulo.
Integración Numérica
No es el propósito de este articulo describir la integración numérica. En las referencias del articulo dispongo algunos enlaces pertinentes para el asunto. El enfoque del articulo esta destinado a un ejemplo concreto del uso de delegados. Digamos de modo general que una ‘integral’ es una función real que calcula el área bajo una curva. Con frecuencia la integral de una función no es simple. Entonces se recurre a técnicas numéricas de aproximación que resultan aceptables en términos de ingeniería. También aplica con frecuencia el calculo de una integral numérica cuando solo se conoce una matriz de datos de la función, y no se conoce su ecuación.
El ejemplo que dispongo en este articulo es un paradigma en donde suponemos que la integral de la función reciproco, f(x) = 1 / x, no es simple y debemos recurrir a técnicas numéricas para su solución. La función integral de f(x) = 1 / x, es conocida como el logaritmo natural de x. Las integrales se evalúan en un intervalo finito, normalmente expresado como integral entre a y b, donde b es mayor que a. Supongamos que a = 1 y b = 2. El ejemplo se concreta así:
Hay varios métodos para determinar el valor de una integral por métodos numéricos. Los más conocidos son la Regla de los Trapecios, y la Regla de Simpson. Encuentra buena información al respecto en las referencias de este articulo. En términos matemáticos los dos métodos se expresan así:
El termino E se refiere al error que implica la técnica numérica. El error tiene una connotación teórica y en la práctica no se aplica. La Regla de Simpson es más precisa que la Regla de los Trapecios, pero se limita a la condición de que n sea impar (el método se basa en aproximación a segmentos de parábola cada 3 punto).
El código de los dos métodos de solución numérica es como sigue. Creo una aplicación de consola con nombre IntegratorSample. Agrego un clase con nombre Integrator, y dispongo el siguiente código:
Ahora, una utilización clásica de esta clase es como se muestra a continuación. Utilizo la clase Program de la aplicación de consola:
Al ejecutar este programa da la siguiente salida:
El valor “exacto” de la integral es ln(2), lo que equivale a: 0.693147180559945... La precisión de la técnica numérica mejora al aumentar el número de trapecios.
Aplicando Delegados
Si estudia la exposición anterior, se puede concluir que se trata de una solución a un problema especifico. Puntualmente se evalúa la integral de la función f(x) = 1/ x por la Regla de los Trapecios. Si quisiéramos resolver otra ecuación por otro método, se podría escribir un bloque de código similar. En programación clásica de producción, podrías escribir un par de enumeraciones, una para los métodos de evaluación, y otra para las ecuaciones que queremos evaluar, e incrustar directivas de selección de caso dentro del código. Si bien los métodos de evaluación tiene un numero discreto, a lo sumo 5 para solución de integrales por técnicas numéricas, el número de ecuaciones es virtualmente infinito. Si deseamos programar una solución general, debemos recurrir a delegados. En la referencia (1) encuentra la documentación MSDN acerca de los delegados.
Para organizar el asunto, diré que hay tres elementos concretos que conforman un delegado.
(1) La declaración del delegado. (2) Las funciones o métodos que hacen juego con los tipos de variables declaradas en el delegado (3) Un función con un parámetro del tipo del delegado declarado
La programación generalizada del problema que expongo se puede tratar en dos partes. Una la solución de delegar el método de cálculo como parámetro, y segundo, delegar la ecuación que se quiere integrar.
Para la primera parte defino el delegado IntergratorRule para invocar el método deseado:
Las funciones SimpsonRule y TrapeziumsRule hacen juego en cuanto a parámetros y tipos devueltos con del delegado IntegratorRule.
Luego se crea la función Integrator, la cual incorpora un parámetro del tipo IntegratorRule:
Nota. Existe la palabra reservada “Invoke” para usar un delegado. Tal vez se ve más en VB.NET que en C#, la sintaxis es opcional, podría haber escrito: “return IR.Invoke(a, b, f);”
De esta manera, disponiendo de la matriz de datos de una función especifica, puedo usar la función Integral pasando como parámetro uno de los métodos de solución (TrapeziumsRule o SimpsonRule) definidos en la clase Integrator, es decir, podría usar la siguiente línea en el ejemplo inicial:
Esto es notablemente más eficiente que definir una función Integrador con un parámetro enumeración con los métodos de cálculo, y pasar el valor de la enumeración como parámetro, el cual se evalúa en una selección de caso dentro de Integrador. Usando delegados evitamos esto y se perciben notoriamente las ventajas de su uso.
Ahora, como segunda parte de la solución, voy a escribir el mecanismo por el cual voy a poder pasar la función que quiero integrar como parámetro. Creo el siguiente delegado en la clase Integrador:
Esto me permitirá llamar por nombre cualquier función de una variable que se defina en alguna clase.
Por ejemplo, construyo una clase de nombre FunctionsSample, a la cual puedo agregar muchas funciones especificas. En el ejemplo incluyo dos, Reciprocal y AnyFunction.
Si, por ejemplo, quiero el reciproco de un numero, digamos 1.234, llamaré la función DoFunction de la siguiente manera
Para finalizar la solución, voy a sobrecargar la función Integrador, para que se pueda llamar tanto el método de cálculo como la función que se quiere integrar. A esta función sobrecarga le implemento la capacidad de que sea la misma función la que calcule los intervalos para solucionar la integral. Agrego el parámetro Divisions con la cual el cliente queda en libertad de establecer la precisión de la integral devuelta. Entre mayor es Divisions, mayor es la precisión del valor devuelto, y mayor el consumo de recursos. En general el valor de Divisions queda dependiendo de las necesidades del cliente. La segunda función Integral queda de la siguiente manera:
Siguiendo el ejemplo, ya se puede escribir la solución generalizada en una línea:
Se puede leer que se ha llamado la función Integral pasando como parámetros el método de calculo y la función que se quiere calcular. El código es loable.
Métodos Anónimos
Con los métodos anónimos se rompe la necesidad de crear una función con nombre para usar un delegado. En versiones de C# anteriores a la versión 2.0, la única manera de usar un delegado es utilizar métodos con nombre. En C# 2.0 y posteriores los métodos anónimos permiten usar un delegado sin escribir una función con nombre. Me explico siguiendo el ejemplo. La función Reciproco se declara en la clase FunctionSample y se delega en MathFuncion. Usando un método anónimo, no tengo necesidad de esto, declaro la función dentro de una variable del tipo de delegación MathFunction. El siguiente ejemplo muestra como:
En el código anterior, declaré la variable f la cual contiene una función anónima, la cual devuelve el reciproco de un numero. Es claro que es supremamente deseable ya que el numero de funciones matemáticas es virtualmente infinito. Si por ejemplo se me presenta la ecuación f(x) = 0.2F * x * x - x + 0.5F, con unas pocas lineas de código soluciono el problema inmediato:
Conclusiones
Los delegados son una característica de los lenguajes .NET que ponen de manifiesto una poderosa herramienta para los desarrolladores. Los delegado aplican loablemente a problemas de ingeniería, simplificando problemas de manera general e intuitiva.
Las soluciones generadas de delegados son más eficaces porque pueden evitar selección de caso dentro de las reglas de negocios.
Notas
Programé la clase Integrador basada en el tipo float. si bien esto aplica cómodamente a problemas de ingeniería, la precisión del tipo float no es conveniente para problemas científicos. No obstante, no es complicado la transformación de float a double de las clases expuestas en el articulo.
El articulo se enfoco a C#, si desea una traducción a VB.NET, no tiene complicación, ni limitaciones. Aparte de cambiar algunas cosas de sintaxis de palabras reservadas, no hay que escribir código más allá del expuesto.
Ejemplo Completo
Puede descargar el ejemplo compreto de la dirección: http://vexpert.mvps.org/sample/IntegratorSample.zip
Referencias
1) Delegados con C#: http://msdn2.microsoft.com/es-es/library/ms173171.aspx 2) Integration: http://www.ping.be/~ping1339/int.htm 3) Numerical integration: http://www.damtp.cam.ac.uk/lab/people/sd/lectures/nummeth98/integration.htm 4) Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra, Tom Apostol
|