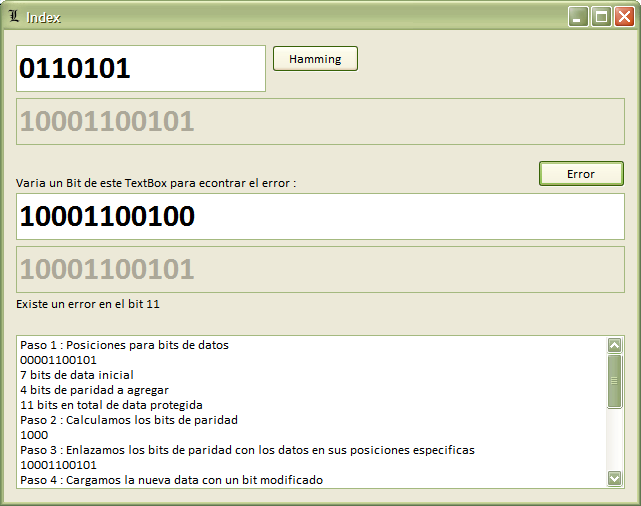
IntroducciónTareas y mas tareas, uff, despues de tiempo que vuelvo a colaborar algo xD, pues me la pase meditando y dizque estudiando (veladas de Dota, tragos y otras delicias de la vida jeje), weno, como es de costumbre en la universidad nos dejan alguna que otra cosa interesante, pues este es uno de los pocos casos, uno de mis profes, (LFL), dejo de trabajo dos temas para investigar de forma grupal (2), del cual solo expondriamos uno, que son el CRC (Código de Redundancia Ciclica) ó el Código Hamming, creo que ya se dieron cuenta cual escogi, o.O, ambos para protección de datos, weno, pequeña protección de datos mientras esta data atraviesa miles de kilometros de cable propenso a la interferencia electromagnetica, etc etc, para no entrar en detalles, aqui dejo nuestro trabajo, que es solo la implementacion de un algoritmo ya conocido. Nota: Nota: Del formulario:
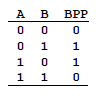
Bueno, ante todo me guie de la informacion que brinda el Wikipedia, es el mismo ejemplo que plantean ahi, procedere a explicar un poco como trabaja este algoritmo, de ante mano, les pediria que revisen el Codigo Hamming para tener un mayor horizonte de lo que se esta haciendo. He variado un poco los pasos designados en el algoritmo, por beneficio propio, teniendo en total 5 pasos, incluida la comprobacion de un bit de error. Paso 1 : armamos el vector y colocamos la data en las posciones adecuadas, (posiciones 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc.) Paso 2 : armamos los minivectores para calcular los bits de paridad, aqui les muestro una imagen de como generalmente se tendrian que armar, cada minivector coge un numero determinado de datos del vector sin coger los bits de paridad. Posición 1: salta 1, comprueba 1, salta 1, comprueba 1, etc. Posición 2: comprueba 1, salta 2, comprueba 2, salta 2, comprueba 2, etc. Posición 4: comprueba 3, salta 4, comprueba 4, salta 4, comprueba 4, etc. Posición 8: comprueba 7, salta 8, comprueba 8, salta 8, comprueba 8, etc. Posición 16: comprueba 15, salta 16, comprueba 16, salta 16, comprueba 16, etc.
Paso 3 : simplemente enlazamos los bits de paridad con el vector de datos, y tendremos como resultado el Vector Hamming Paso 4 : comenzamos con la comprobación, ahora modificaremos un bit. Paso 5 : calculamos la posicion del bit erroneo, gracias a los bits de paridad analizaremos y los bits de paridad nos devolveran el numero de bit erroneo para su corrección. El código:Creo que todas las funciones aqui elaboradas, son entendibles, de igual forma, solo explicare razgos generales del codigo *Funcion necesaria para el paso 1.
'Funcion para convertir de binario a texto o texto a binario segun la opcion de direccion
'se recibe un vector de datos boleanos
Function BinTexTexBin(ByVal Vector() As Boolean, ByVal Texto As String, ByVal mk As Integer, ByVal Direccion As Boolean)
Dim i As Integer
'Si direccion = true, entonces se convertira de texto a binario, y se devolvera un vector
If Direccion = True Then
For i = 1 To Texto.Length
If Texto(i - 1).ToString = 1 Then
Vector(i) = True
Else
Vector(i) = False
End If
Next i
Return Vector
'Si direccion = false, entonces se convertira de binario a texto, y se devolvera un string
'siguiendo el formato Big Endian
Else
Texto = ""
For i = 1 To mk
If Vector(i) = True Then
Texto = Texto + "1"
Else
Texto = Texto + "0"
End If
Next i
Return Texto
End If
End Function
*Funcion necesaria para el paso 1.
'Funcion para armar posiciones de la data, en este caso la data debe ir en las posiciones
'que no son multiplos de 2^k, (posiciones 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc.)
Function ArmarPosiciones(ByVal Vector() As Boolean, ByVal m As Integer)
Dim VPosicion(2 * m + 1) As Boolean
Dim i, c, mk, Potencia As Integer
Dim Centinela As Boolean = False
i = 3
c = 1
Potencia = 2
While c <= m And Centinela = False
VPosicion(i) = Vector(c)
If c <> m Then
c = c + 1
i = i + 1
If i = Pow(2, Potencia) Then
Potencia = Potencia + 1
i = i + 1
End If
Else
Centinela = True
End If
End While
mk = i
Clipboard.SetText(mk.ToString)
Return VPosicion
End Function
*Funcion necesaria para el paso 2,4.
'Funcion para sacar los minivectores que son necesarios para el calculo de cada bit de paridad
'Posición 1: salta 1, comprueba 1, salta 1, comprueba 1, etc.
'Posición 2: comprueba 1, salta 2, comprueba 2, salta 2, comprueba 2, etc.
'Posición 4: comprueba 3, salta 4, comprueba 4, salta 4, comprueba 4, etc.
'Posición 8: comprueba 7, salta 8, comprueba 8, salta 8, comprueba 8, etc.
'Posición 16: comprueba 15, salta 16, comprueba 16, salta 16, comprueba 16, etc.
Function ArmarSecuenciaPar(ByVal Vector() As Boolean, ByVal Index As Integer, ByVal mk As Integer, ByVal m As Integer)
Dim VSecuencia(m) As Boolean
Dim Cantidad As Integer = Pow(2, Index)
Dim i, c, Terminos, Puntero As Integer
i = 1
For c = Cantidad To mk Step 2 * Cantidad
VSecuencia(i) = Vector(c)
Puntero = c
Terminos = 1
While Terminos < Cantidad
Terminos = Terminos + 1
i = i + 1
If (i <= m) And (Puntero + 1 <= mk) Then
VSecuencia(i) = Vector(Puntero + 1)
End If
Puntero = Puntero + 1
End While
i = i + 1
Next c
Return VSecuencia
End Function
*Funcion necesaria para el paso 2,4. gracias a la funcion xor.
'Funcion generadora de paridad entre 2 bits
Function GParidadPar(ByVal A As Boolean, ByVal B As Boolean) As Boolean
GParidadPar = A Xor B
Return GParidadPar
End Function
*Funcion necesaria para el paso 2,4.
'Funcion recursiva para determinar la paridad de los minivectores
'generados para cada bit de paridad
Function DetParidad(ByVal Vector() As Boolean, ByVal m As Integer) As Boolean
Dim i As Integer
If m <= 1 Then
DetParidad = Vector(m)
Return DetParidad
End If
DetParidad = GParidadPar(Vector(1), Vector(2))
If m <= 2 Then
Return DetParidad
End If
For i = 3 To m
DetParidad = GParidadPar(DetParidad, Vector(i))
Next i
Return DetParidad
End Function
*Funcion necesaria para el paso 3.
'Funcion que enlaza el vector de datos con el vector de paridades
'en sus posiciones designadas
Function ArmarSecuenciaYParidad(ByVal Vector() As Boolean, ByVal VParidad() As Boolean, ByVal m As Integer, ByVal k As Integer)
Dim VHamming(m + k) As Boolean
Dim i, c As Integer
i = 1
c = 1
While (i <= (m + k)) And (c <= k)
Vector(i) = VParidad(c)
i = Pow(2, c)
c = c + 1
End While
VHamming = Vector
Return VHamming
End Function
*Funcion necesaria para el paso 5.
'Funcion para convertir un binario a su representacion en numero entero
'siguiendo el formato Big Endian
Function BinarioANumero(ByVal Binario As String) As Integer
Dim Tamano, i, c As Integer
BinarioANumero = 0
Tamano = Binario.Length
c = Tamano
For i = Tamano To 1 Step -1
If Binario(i - 1).ToString = 1 Then
BinarioANumero = Pow(2, i - 1) + BinarioANumero
Else
BinarioANumero = BinarioANumero
End If
Next i
Return BinarioANumero
End Function
Creo que todo esta claramente explicado, como siempre, solo explico las funciones, el codigo interno del formulario lo envio en el archivo. uff, pos espero seguir aportando, me disculpo por perderme, pero es mi costumbre hacerlo xD, jaja, nos vemos hasta la proxima colaboración, chaitos!!! Espacios de nombres usados en el código de este artículo:Libreria utilizada System.Math Sobre el Autor:
|