Este graficador de funciones nace de la idea o tal vez necesidad de presentarlo en un proyecto final de un curso en la universidad, mejor dicho en mi universidad (Universidad Nacional de Trujillo), aqui  en Perú. Sé que para mucho de ustedes amigos avanzados en .NET, se le debe hacer algo sencillo realizar lo que yo hice "heroicamente"  en una noche que nunca olvidaré, se suponía en ese momento de angustía y desesperación, en donde si este programa no corría entonces estaba muerto. Sucede que confiaba mucho en mí, y eso me animó echar siempre pa'lante (para adelante), al final todo salió muy bien y el graficador funcionó correctamente...jejeje..Vale la pena resaltar que el graficador que se presentó en el proyecto lo desarrollé en c++, ya que no es tan sencillo en este lenguaje...., felizmente como buen programador tengo las ideas bien puestas y será el fruto del código binario lo que cosecharé, con el pasar del tiempo, y no calificaciones , es decir, en la programación ó  eres un uno ó eres un cero, tú eliges.

Inevitablemente, la vida de un programador se caracteriza por su constante aprendizaje, un programador que desee estar a la par y siempre al día sufrirá de la "maldición eterna" del estudio. La situación real es que, el área de la informática avanza a tal velocidad que tomar un descanso de un par de semanas pueden significar que ahora estes al final de la fila, cuando, tal vez, una vez estuviste al principio. Es debido a esto que debemos buscar ciertos patrones de comportamiento positivos para realizar prácticas de programación que nos ayuden a desarrollar software de una manera eficiente y muy rápida.

Aprendí a programar a los 16 años (empecé con PASCAL), actualmente vivo muy empeñoso con .NET, al principio fue una cosa rara todo esto de la programación pero todo cambió, ahora es algo muy común para mi. Con esto quiero decirte que, una vez  que aprendes a programar es siempre cuestión de como saber traducir tus ideas al dialecto programático en el cual estés interesado. Se trata simplemente de sentarte frente a tu PC y hablarle en el lenguaje  que esta entienda, es más, tú puedes elegir en  que dialecto o lenguaje hablarle y ordenarle lo que  desees, piensa que el ordenador es tu amigo y a la vez tu empleado..jejejeje.... 

Esta vez no quiero demostrate un descubrimiento en la programación gráfica o algún aspecto marcianamente complejo, sino más bien, quiero mostrarte sencillamente la manera como desarrollé un graficador de funciones en VB .net, el cual es interesante debido a la lógica que utilicé. Si sabes alguna manera distinta de desarrollar un graficador pues escríbeme al correo. Además, debo decirte que este documento recoge ideas, estilos y maneras de hacer fáciles las cosas "complejas" de la programación, la cual comparto con ustedes  de tal forma que puedan aprovecharlos. Quiero dejar constancia que parte del contenido de esta página fue tomada de un curso de programación gráfica, mejor dicho tan sólo la teoría, ya que el graficador lo implementé yo, tomando sólo algunas pautas que este curso me brindaba. Bueno, para aprender a realizar prácticas de programación gráfica, debemos empezar por saber lo más básico, cuya información al respecto sigue a continuación.

Trazar Ecuaciones

Para comenzar, veamos un ejemplo práctico del uso de gráficos: trazar la gráfica de una ecuación. En este capítulo trazaremos la ecuación: y = 3x² - 6. Como ya sabemos, esta ecuación describe una parábola cóncava (hacia "arriba") - en el sentido positivo por el eje-Y. Nosotros, como matemáticos, trazamos tal gráfica tomando ciertos valores de x para calcular valores de y y así crear coordenadas por donde pasará la gráfica. Al ser humanos, no nos gusta tomar todos los posibles valores, por lo que creamos una tabla de valores calculando algunas coordenadas, hasta que tengamos una idea de dónde situar la gráfica. En nuestra ecuación, sabemos de antemano que se trata de una parábola, por lo que ya conocemos su forma y estructura. En papel, aproximamos el trazado a la gráfica real, ya que no nos hace falta tanta precisión; o sea, lo hacemos a ojo de buen cubero. Sin embargo, esto no es posible al crear la gráfica en pantalla: necesitamos ser precisos.

Cambio de Coordenadas   

La ventaja que tenemos es que el ordenador no se "cansará" al calcular todos los valores que requerimos, por lo que no tendremos problemas de precisión. Por otro lado, estamos intentado representar una imagen de dimensiones infinitas - el plano cartesiano, debido a los valores de x que son infinitos, en un área de dimensiones finitas - la pantalla. Por lo tanto, debemos representar la gráfica ajustándonos a las dimensiones de nuestra pantalla. Las dimensiones de la imagen equivalen a la resolución gráfica establecida. Para este ejemplo, usaremos una resolución de 800x600.

Ahora tenemos que pensar qué representa cada píxel que activemos - demos color. Si establecemos que cada píxel equivale a una unidad matemática, entonces no obtendremos una imagen presentable. Hay que tener en cuenta que las unidades matemáticas no tienen por qué ser valores enteros, mientras que los píxeles sí deben serlos. Lo que tenemos que hacer es decidir los valores mínimos y máximos a usarse en la ecuación. Digamos que queremos ver parte de la gráfica usando los valores de x : [-3, +3]; o sea, x_ui = -3 y x_uf = 3, los cuales representan los valores mínimos y máximos de las unidades del plano cartesiano, respectivamente. Aún así, no podemos usar todos los valores en este conjunto, ya que serían infinitos. Como ya sabemos, no podemos representar valores infinitos en un sistema de valores finitos (limitados). Tenemos que repartir estos valores cartesianos de entre los posibles valores de la pantalla del mismo eje X; es decir, tenemos que conseguir cambiar el intervalo [-3, +3] al de [0, 799]. Los valores iniciales y finales son fáciles de averiguar: x_ui = -3 => 0 y x_uf = 3 => 799. Los demás valores deberán ser calculados:
Primeramente, debemos cambiar la escala o longitud: 6 (=3-(-3)) unidades cartesianas a 800 píxeles (el número de columnas); esto implica que existen 6/800 unidades cartesianas por cada píxel, que es lo mismo que decir: 0,0075 unidades/píxel. Dicho de otro modo, cada píxel representará 0,0075 unidades cartesianas. Miremos unos cuantos valores, para ilustrar este concepto:

Valores de X

Unidades Cartesianas	Píxeles
-3,0000	0
-2,9925	1
-2,9850	2
-2,9775	3
. . .	. . .
2,9700	796
2,9775	797
2,9850	798
2,9925	799

También podemos establecer la relación realizando la operación inversa: 800/6 = 133,3333 píxeles/unidad. Aquí podemos ver que sería algo difícil representar 133,3333 píxeles, ya que los píxeles son siempre enteros. Esto implica que obtendremos errores al aproximarnos a un número entero; en este caso, 133 (~133,3333).

Cual sea la relación, podemos averiguar un píxel determinado a partir de una coordenada cartesiana determinada, y viceversa. Por ejemplo, si tenemos la coordenada-X de un píxel, x_p = 345, para poder averiguar el valor de x en unidades cartesianas, realizamos la siguiente operación:

 6 unidades         |xu - xui| unidades
-------------  =  ---------------------- =>
 800 píxeles        |345 - xpi| píxeles

|345 - 0| píxeles * 0,0075 unidades/píxel = |x - (-3)| unidades =>

x = -0,4125 unidades.

Por otro lado, podemos averiguar el píxel correspondiente a la coordenada-X, x_u = -2,0000, aplicando la simple regla de tres:

 800 píxeles          |xp - xpi| píxeles
-------------  =  -------------------------- =>
 6 unidades        |-2,0000 - xui| unidades

1,000 unidad * 133,3333 píxeles/unidad = |xp - 0| píxeles =>

x = 133,3333 píxeles => x = 133 píxeles.

Del mismo modo, tenemos que averiguar los valores de y en unidades cartesianas correspondientes con los valores en píxeles. El número de filas es 600 píxeles, según nuestra resolución que hemos elegido. Ya que los valores del eje-Y son imaginarios, éstos pueden ser calculados. Por esta razón, el conjunto de valores puede ser ajustado según los valores inicial y final del eje-X. Con x_ui = -3, obtenemos y_u = 3 (x_ui)² - 6 => y_u = 21. Con x_uf = 3, obtenemos y_u = 21. Ahora averiguaremos la coordenada del valor mínimo de y_u de la curva con la siguiente fórmula: 6x_u = 0 => x_u = 0, y por tanto, y_u = -6.  La fórmula usada proviene de la derivada de nuestra ecuación: y_u = 3 (x_u)² - 6, para averiguar el punto crítico. Ahora tenemos que los valores de y se encuentran entre [-6, +21]; esto es, y_ui = -6 e y_uf = +21. Por lo tanto, necesitamos realizar otro cambio de escala: 27 (=21-(-6)) unidades cartesianas a 600 píxeles (el número de filas). Esto quiere decirse que tenemos 27/600 = 0,0450 unidades/píxel. Veamos unos cuantos valores:

Valores de Y

Unidades Cartesianas	Píxeles
-6,0000	0
-5,9550	1
-5,9100	2
-5,8650	3
. . .	. . .
20,8200	596
20,8650	597
20,9100	598
20,9550	599

Calculemos el píxel que corresponda al valor en unidades cartesianas de y_u = 3 (-2,000)² - 6 => y_u = 6,000. Nuevamente se trata de aplicar la regla de tres con la información que tenemos:

 600 píxeles           |yp - ypi| píxeles
-------------  =  -------------------------- =>
 27 unidades        |6,0000 - yui| unidades

|6,0000 - (-6)| unidades * 22,2222 píxeles/unidad = |yp - 0| píxeles =>

y = 266,6666 píxeles => y = 267 píxeles.

Hasta aquí es la teoría, ahora, les muestro el código del ejemplo que implementé en Microsoft® Visual Basic .NET®. Pero antes debo decirle que la cuestión de resolución gráfica, los límites de la función a graficar, los puntos máximos y mínimos, y otros detalles, fueron manejadas de acuerdo a mi estilo personal. Para los curiosos, este graficador se basa en una resolución gráfica de 1024x768 píxeles, te comunico esto para evitarte molestias al momento de probarlo.

Al revisar el código notarás que existe un algoritmo que implementé para calcular los puntos máximo y mínimo de la función, si quieres saber de se trata este algoritmo entonces te recomiendo buscar en la web toda información con respecto a optimización de funciones, en especial "Método de la Sección Dorada", la cual uso para hallar estos puntos... bueno esto yo lo aprendí en la universidad.

Cuando el programa empieza graficar la función, lo hace de una manera progresiva y dinámica, empleando para esto un ProgressBar para ir mostrando al usuario el avance del trabajo. ¿...interesante, verdad...?.

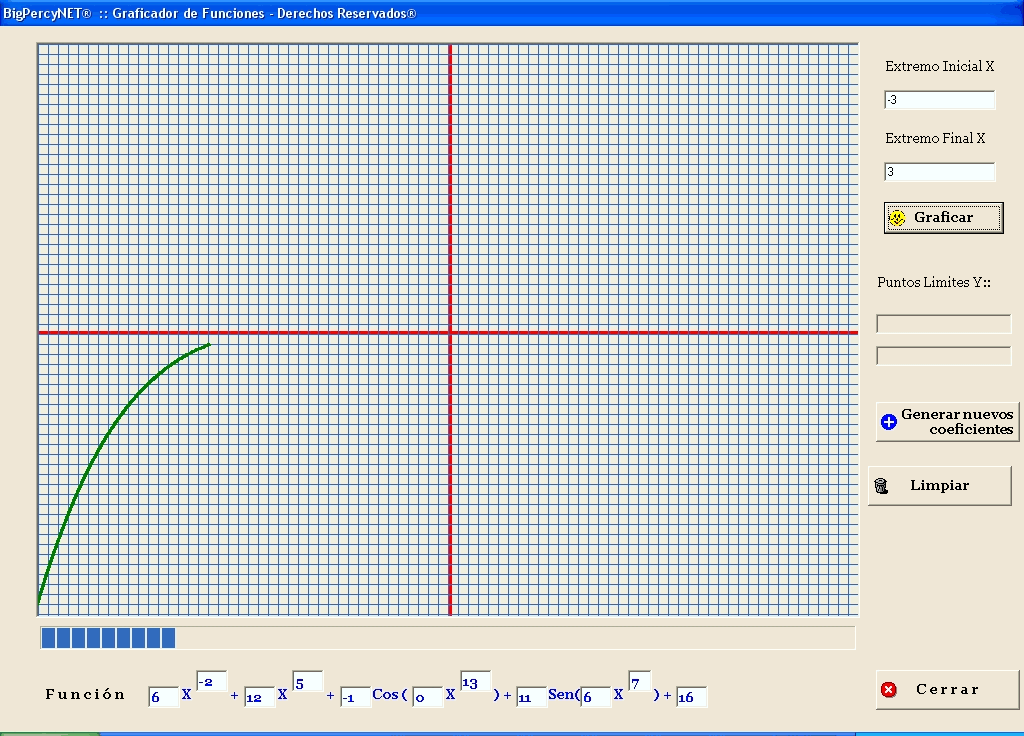
....luego observamos que la construcción de la gráfica está yendo por bueno camino, siguiendo el avance de toda la gráfica  mediante el ProgressBar. De esta manera, hacemos el trabajo algo más divertido. 

 

Finalmente, observamos que la construcción ha concluido con éxito, nuestra función ha sido graficada. También se puede ver que al final  de este proceso se muestra un mensaje parpadeante avisándonos que todo  ha salido bien, además visualizaremos los puntos máximo y mínimo de la función. Un detalle importante es que podemos medir el tiempo empleado para realizar la gráfica. Bueno hasta aquí ha sido todo  el "chiste"....

A continuación sigue código en Microsoft® Visual Basic .NET®:

Imports System.Drawing.Drawing2D
Imports System.Math

Public Class Form1
    Inherits System.Windows.Forms.Form
 <STAThread()> Shared Sub main()
        Try
            Application.Run(New Form1)
        Catch ex As Exception
            MsgBox("Cuidado :: " & ex.Message)
        End Try
    End Sub

    Public Shared a, b, c, d, e, f, g, h, i, j, k, m, constante As Single

    Public Function NetFuncion(ByVal X As Double) As Double
        'capturo los coeficientes...
        a = CType(Me.TextA.Text, Single)
        b = CType(Me.TextB.Text, Single)
        c = CType(Me.TextC.Text, Single)
        d = CType(Me.TextD.Text, Single)
        e = CType(Me.TextE.Text, Single)
        f = CType(Me.TextF.Text, Single)
        g = CType(Me.TextG.Text, Single)
        h = CType(Me.TextH.Text, Single)
        i = CType(Me.TextI.Text, Single)
        j = CType(Me.TextJ.Text, Single)
        constante = CType(Me.TextConstante.Text, Single)
        'reemplazo los coeficientes en la función...
        Return a * Pow(X, b) + c * Pow(X, d) + e * Cos(f * Pow(X, g)) + h * _
        Sin(i * Pow(X, j)) + constante
    End Function

    Private Sub Form1_Load(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles MyBase.Load
        'manipulo algunas propiedades...
        Me.ControlBox = False
        Me.PictureBox1.BackColor = SystemColors.ControlLight
        Me.WindowState = FormWindowState.Maximized
        'defino la posición y tamno incial para el PictureBox1...
        Me.PictureBox1.Location = New Point(Me.Location.X + 40, Me.Location.Y + 20)
        Me.PictureBox1.Size = New Size(Me.ClientSize.Width - 200, Me.ClientSize.Height - 130)
        'genero aleatoriamente los coeficientes...
        Me.BtnGenCoef.PerformClick()
    End Sub

    'procedimiento para dibujar la cuadricula de fondo...
    Public Sub Cuadricula()
        'dibujamos la coordenada Y
        Me.PictureBox1.CreateGraphics.DrawLine(New Pen(Color.Red, 3), _
        New PointF(Me.PictureBox1.Width / 2, 0), _
        New PointF(Me.PictureBox1.Width / 2, Me.PictureBox1.Height))
        'dibujamos la coordenada X
        Me.PictureBox1.CreateGraphics.DrawLine(New Pen(Color.Red, 3), _
        New PointF(0, Me.PictureBox1.Height / 2), _
        New PointF(Me.PictureBox1.Width, Me.PictureBox1.Height / 2))
        'dibujo de toda cuadricula
        Dim NroLines As Integer = 0
        'lineas horizontales de la cuadrícula de fondo
        For NroLines = 0 To Me.PictureBox1.Height Step 10
            Me.PictureBox1.CreateGraphics.DrawLine(New Pen(SystemColors.Highlight, 1), _
            New Point(0, NroLines), New Point(Me.PictureBox1.Width, NroLines))
        Next
        'lineas verticales de la cuadrícula de fondo
        For NroLines = 0 To Me.PictureBox1.Width Step 10
            Me.PictureBox1.CreateGraphics.DrawLine(New Pen(SystemColors.Highlight, 1), _
            New Point(NroLines, 0), New Point(NroLines, Me.PictureBox1.Height))
        Next
    End Sub

    Public Function CalculateMaxAndMin(ByVal modo As Integer) As Single
        'algoritmo de optimización MÉTODO DE LA SECCIÓN DORADA
        'Sirve para hallar los punto máximo y mínimo de la función
        'que queremos graficar...
        Dim a, b, sol As Single
        'sol... viene a ser el valor X que se tomará como abscisa
        'para calcular el máximo y mínimo
        a = CType(TxtXini.Text, Single)
        b = CType(TxtXfin.Text, Single)
        Dim x1, x2, funx1, funx2 As Single
        Dim tol As Single = 0.00001
        Dim r As Single = 0.618
        Dim ErrorNet As Single
        ErrorNet = (1 - r) * (b - a)
        While (tol < ErrorNet)
            x1 = a + r * (b - a)
            x2 = b - r * (b - a) 

             If modo * NetFuncion(x1) > modo * NetFuncion(x2) Then
                a = x2
                ErrorNet = b - x1
                sol = x1
            Else
                b = x1
                ErrorNet = x1 - x2
                sol = x2 

          End If
        End While
        'finalmente devolvemos el valor de máximo o mínimo,
        'Nota: la variable "modo" determina de que si hallemos el máximo o el mínimo
        Return NetFuncion(sol)
    End Function

    Function Maximo() As Single
        Return CalculateMaxAndMin(1)
    End Function

    Function minimo() As Single
        Return CalculateMaxAndMin(-1)
    End Function

    'procedimiento para graficar la función...
    Public Sub GraficarFuncion()
        Cuadricula()
        Dim XMinUnidCartesianas, XMaxUnidCartesianas As Single
        Dim YminUnidCartesianas, YMaxUnidCartesianas As Single
        Dim XFinPixel, XIniPixel, YFinPixel, YIniPixel As Single
        Dim X = 0, Y = 0, Yp = 0, Xp As Single
        Dim X1, min, max As Single
        Dim c As Single = 0.0001
        XIniPixel = Me.PictureBox1.Location.X
        XFinPixel = XIniPixel + Me.PictureBox1.Size.Width
        YIniPixel = Me.PictureBox1.Location.Y
        YFinPixel = YIniPixel + Me.PictureBox1.Size.Height
        XMinUnidCartesianas = CType(TxtXini.Text, Single)
        XMaxUnidCartesianas = CType(TxtXfin.Text, Single)
        YminUnidCartesianas = minimo()
        YMaxUnidCartesianas = Maximo()
        Application.DoEvents() 

        Me.ProgressBar1.Maximum = Math.Abs(XMaxUnidCartesianas - XMinUnidCartesianas)
        Dim i As Single = 0
        For X1 = XMinUnidCartesianas To XMaxUnidCartesianas Step c
            If i <= Math.Abs(XMaxUnidCartesianas - XMinUnidCartesianas) Then
                Application.DoEvents()
                Me.ProgressBar1.Value = i
                i += c
            End If
            X = X1 : Y = NetFuncion(X)
            'tranformamos nuestras coordenadas cartesianas a píxeles
            'Xp = valor de la coordenada X en píxeles...
            Xp = XIniPixel + Pow(Pow(((XFinPixel - XIniPixel) * (X - XMinUnidCartesianas)) / _
            (XMaxUnidCartesianas - XMinUnidCartesianas), 2), 0.5)
            Yp = YIniPixel + Pow(Pow(((YFinPixel - YIniPixel) * (Y - YminUnidCartesianas)) / _
            (YMaxUnidCartesianas - YminUnidCartesianas), 2), 0.5)
            Dim PuntoInicial As PointF = New PointF(Xp - 40, Me.PictureBox1.Height - Yp + 10)

            X = X1 + c : Y = NetFuncion(X1 + c) 

             'Yp=valor de la coordenada Y en píxeles...
            Xp = XIniPixel + Pow(Pow(((XFinPixel - XIniPixel) * (X - XMinUnidCartesianas)) / _
            (XMaxUnidCartesianas - XMinUnidCartesianas), 2), 0.5)
            Yp = YIniPixel + Pow(Pow(((YFinPixel - YIniPixel) * (Y - YminUnidCartesianas)) / _
            (YMaxUnidCartesianas - YminUnidCartesianas), 2), 0.5)
             Dim PuntoFinal As PointF = New PointF(Xp - 40, Me.PictureBox1.Height - Yp + 10)

            Try
                Me.PictureBox1.CreateGraphics.DrawLine(New Pen(Color.Green, 3), _
                PuntoInicial, PuntoFinal)
            Catch ex As Exception
                Me.PictureBox1.CreateGraphics.DrawLine(New Pen(Color.Green, 3), 0, 0, 0, 0)
            End Try
        Next
        'dibujamos la cuadrícula...
        Cuadricula()
    End Sub

    Private Sub BtnLimpiar_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles BtnLimpiar.Click
        Me.PictureBox1.Invalidate()
    End Sub

    Private Sub BtnGenCoef_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles BtnGenCoef.Click
        'genereamos valores inciales para los coeficientes...
        Randomize()
        Me.LabelTIEMPO.Visible = False
        Dim ran As New Random
        Me.TextA.Text = ran.Next(-2, 20)
        Me.TextB.Text = ran.Next(-2, 20)
        Me.TextC.Text = ran.Next(-2, 20)
        Me.TextD.Text = ran.Next(-2, 20)
        Me.TextE.Text = ran.Next(-2, 20)
        Me.TextF.Text = ran.Next(-2, 20)
        Me.TextG.Text = ran.Next(-2, 20)
        Me.TextH.Text = ran.Next(-2, 20)
        Me.TextI.Text = ran.Next(-2, 20)
        Me.TextJ.Text = ran.Next(-2, 20)
        Me.TextConstante.Text = ran.Next(-2, 20)
    End Sub

    Private Sub BtnSalir_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles BtnSalir.Click
        Me.Close()
    End Sub

    Private Sub BtnGraficar_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles BtnGraficar.Click
        Me.Label4.Visible = False
        Me.Timer1.Enabled = False
        Me.Timer2.Enabled = False
        'tiempo en que se empieza a graficar la función
        Dim TiempoInicial As Date = System.DateTime.Now
        'graficamos la función..
        GraficarFuncion()
        'tiempo en que se termina graficar la función
        Dim TiempoFinal As Date = System.DateTime.Now
        Me.LabelTIEMPO.Visible = True
        'calculamos el tiempo en segundos empleados para realizar la grafica...
        Me.LabelTIEMPO.Text = "Tiempo :: " & DateDiff(DateInterval.Second, TiempoInicial, _
        TiempoFinal).ToString & " Segundos."
        'mostramos los valores máximo y mínimo
        Me.TextBox1.Text = "MaximoY: " & Maximo()
        Me.TextBox2.Text = "MinimoY: " & minimo()
        Me.Timer1.Enabled = True
    End Sub

    Private Sub Timer1_Tick(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles Timer1.Tick
        Me.Timer1.Enabled = False
        Me.Label4.Visible = False
        Me.Timer2.Enabled = True
    End Sub

    Private Sub Timer2_Tick(ByVal sender As System.Object, ByVal e As System.EventArgs) _
        Handles Timer2.Tick
        Me.Timer2.Enabled = False
        Me.Label4.Visible = True
        Me.Timer1.Enabled = True
    End Sub
End Class

Nuevamente como siempre deseo que este trabajo haya sido de tu agrado y contribuido en mejorar tu experiencia como programador. Consideró importante expresar mis agradecimientos sinceros a El Guille por brindarme la oportunidad de expresearme al mundo programático a través de su web site, en verdad muchas gracias. Por ahora estoy "despertándo" en el mundo de la programación, debido a esto colaboro contigo, más adelante quizás no sea habitual  esto, debido a la disponibilidad de tiempo, pero siempre deseo ayudarte para que todos mejoremos. Cualquier consulta será bienvenida. Hasta pronto. Tu amigo Percy Reyes.

No olvides de darme tu voto en PanoramaBox, de esta manera seguiré compartiendo contigo lo que voy aprendiendo. Gracias

---

Espacios de nombres usados en el código de este artículo:

Imports System.Drawing.Drawing2D
Imports System.Math

Fichero con el código de ejemplo: Percynet_Graficador.zip - Tamaño 32 KB